 |
| One type of Mayan Calendar. Photo by Jasmin Gimenez |
LDS Mesoamerican scholars John L. Sorenson, John E. Clark, Brant A. Gardner, and Mark Alan Wright have all discussed various ways Nephite years might actually be 360-day tuns of the Mesoamerican Long Count calendar.[1]In his article on dating the death of Jesus Christ, ancient Near Eastern archaeologist Jeffrey R. Chadwick disputed this suggestion. Chadwick asserted, “There is no indication that the Maya thought of their tun count as a ‘year,’” and that “[Michael D.] Coe does not refer to the tun as a ‘year’ anywhere in his discussion of the Mayan calendar system.”[2]
Unfortunately, Chadwick has not done enough research on the Mesoamerican Long Count. Coe himself does not call the tun a year, but several other scholars do. Mary Miller and Karl Taube, for instance, explained the Long Count as follows:
Periods of time were counted by days, periods of 20 days (the uinal), years—sometimes called “computing years by archaeologists”—of 360 days (the tun), 20-year periods of 360 days each (the katun), and 400-year periods (the baktun).[3]
Joel W. Palka said the Long Count “is calculated by multiplying a certain number by five different periods: baktun, or 400 years(360 days), katun, or 20 years, tun, or a year, uinal, or a month (20 days), and kin, or a day.”[4]Kaylee Spencer and Linnea H. Wren use the heading “Winal and Tun: Month and Year,” to title the section of their paper on those time periods in the Long Count system.[5]
The use of 360 days deliberately broke from the standard pattern of the Long Count in order to better approximate a year, according to Anthony F. Aveni.
To reckon deep time, the Maya created the longest Mesoamerican calendar cycle by multiplying the basic unit of twenty to the fifth order, the exception being the multiplication of the 20-day count by 18 to form a cycle of 360 days, or one tun, which approximated the year.[6]
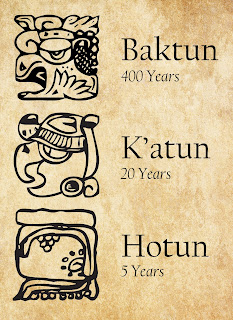 |
| Glyphs for various Long Count periods. Image by Jasmin Gimenez |
Lars Kirkhusmo Pharo similarly explained that the 360-day cycle in the Long Count “was the fundamental unit intended to approximate the solar or vague year of 365 days.”[7]
The Maya even used the same word for both the 360-day period and the 365-day solar year, according to Michael D. Coe and Stephen Houston. After describing the “‘Vague Year or Ha’b of 365 days,” they discussed the Long Count system and noted, “in a switch sure to confuse modern readers, the tun was really called ha’b!”[8] Pharo presented the Long Count system “with Yucatec designations in parenthesis” as follows:
Pik (Bak’tun): 144,000 days
Winikhaab (K’atun): 7,200 days
Haab (Tun): 360 days
Winal/Winik: 20 days
K’in: 1 day[9]
Notice, again, that haab is equivalent to tun. In a footnote, Pharo mentioned of the “haab of 360 days,” and also explained, “Tun is the Yucatec word for haab, which is a Yucatec designation for a year of 365 days.”[10]
Today, it is a scholarly convention to use haab for the 365-day year and tun for the 360-day year (I assume to avoid confusion), but in pre-Columbian times, both terms were used for both the 365-day and360-day periods—one (haab or h’ab) being the lowland Maya term, the other (tun) being the Yucatec term.
So for all intents and purposes, the Maya did call the 360-day period a “year.” Of course, this does not mean that the Book of Mormon year was the 360-day tun, but it does illustrate that Chadwick’s reasons for rejecting that possibility are not well founded.
[1] John L. Sorenson, An Ancient American Setting for the Book of Mormon (Salt Lake City and Provo, UT: Deseret Book and FARMS, 1985), 272–274; John L. Sorenson, Mormon’s Codex: An Ancient American Book (Salt Lake City and Provo, UT: Deseret Book and Neal A. Maxwell Institute for Religious Scholarship, 2013), 440; John E. Clark, “Archaeology, Relics, and Book of Mormon Belief,” Journal of Book of Mormon Studies 14, no. 2 (2005): 46–47; John E. Clark, “Archaeological Trends and Book of Mormon Origins,” in The Worlds of Joseph Smith: A Bicentennial Conference at the Library of Congress, ed. John W. Welch (Provo, UT: BYU Press, 2005), 90; Brant A. Gardner, Second Witness: Analytical and Contextual Commentary on the Book of Mormon, 6 vols. (Salt Lake City, UT: Greg Kofford Books, 2007), 1:362–364, 4:595, 5:176–177; Mark Alan Wright, “Nephite Daykeepers: Ritual Specialists in Mesoamerica and the Book of Mormon,” in Ancient Temple Worship: Proceedings of the Expound Symposium, 14 May 2011, ed. Matthew B. Brown, Jeffrey M. Bradshaw, Stephen D. Ricks, and John S. Thompson (Salt Lake City and Orem, UT: Eborn Books and Interpreter Foundation, 2014), 253.
[2] Jeffrey R. Chadwick, “Dating the Death of Jesus Christ,” BYU Studies 54, no. 4 (2015): 147 n.45, 145 n.43. Chadwick cited Michael D. Coe, The Maya, 8th edition (New York, NY: Thames and Hudson, 2011), 62–69, 231–235.
[3] Mary Miller and Karl Taube, An Illustrated Dictionary of the Gods and Symbols of Ancient Mexico and the Maya (New York, NY: Thames and Hudson, 1993), 50, bolding added.
[4] Joel W. Palka, The A to Z of Ancient Mesoamerica (Lanham, MD: Scarecrow Press, 2010), 22, bolding added.
[5] Kaylee Spencer and Linnea H. Wren, “Arithmetic, Astronomy, and the Calendar,” in Lynn V. Foster, Handbook to Life in the Ancient Maya World (New York, NY: Oxford University Press, 2002), 257, bolding added.
[6] Anthony F. Aveni, “Mesoamerican Calendars and Archaeoastronomy,” in The Oxford Handbook of Mesoamerican Archaeology, ed. Deborah L. Nichols and Christopher A. Pool (New York, NY: Oxford University Press, 2012), 788–789.
[7] Lars Kirkhusmo Pharo, The Ritual Practice of Time: Philosophy and Sociopolitics of Mesoamerican Calendars(Boston, MA: Brill, 2014), 19 n.4.
[8] Michael D. Coe and Stephen Houston, The Maya, 9th edition (New York, NY: Thames and Hudson, 2015), 64, 67; also see p. 260: “a tun, or in Classic times, ha’b, of 360 days.” I do not have access to a copy of the 8th edition, which Chadwick cited, so I do not know if this detail is included in the edition Chadwick was using.
[9] Pharo, Ritual Practice of Time, 19, bolding added.
[10] Pharo, Ritual Practice of Time, 19 n.4.
Continue reading at the original source →



