Yesterday, I posted a link to a great discussion about COVID-19 testing, and the various types of tests that do or will exist, and their strengths/weaknesses.

It can strike many people as strange that doctors’ tests aren’t 100% accurate. (It even surprises some doctors!) No test is perfect.

But, not only are tests not perfect, but even a test that sounds like its very accurate can be misleading if used under the wrong conditions.

Bayes’ Theorem

Bayes’ theorem is enormously important in statistics. In plain English, it sets out to answer the following question:

If I am X% sure before I do a test that someone has Condition A, how much more sure am I after the test is positive? OR

If I am X% sure before I do a test that someone DOES NOT have Condition A, how much more sure am I after the test is negative?

Think of it this way: let’s say you have a 1 in 1 billion chance of having a given disease. I do a test that has a 5% false positive rate–that is, 5% of the times I get a positive answer, it is a mistake in the test.

So, you walk in off the street and I test you–and you test positive. Should you panic?

No–because the chance of you having a false positive (1 in 20 such results) is far, far higher than your chance of having the disease (1 in 1 billion).

So why did I do the test? Because I’m an idiot, and a bad doctor. I shouldn’t have done it. It tells me virtually nothing, and it worries you for no purpose.

A real-life example, colour-coded

To make this more clear, let’s look an example of antibody testing for COVID-19 immunity. This is discussed in detail in the link I provided above.

These tests aren’t perfect, and they can’t be. There’s basically something on the test binding to the antibody we want to detect. We use exactly the same technology for pregnancy tests–we bind to the pregnancy hormone beta-hCG.

The reason they can’t be perfect is because we all have millions of different antibodies in our blood. There’s going to be some risk that, by random chance, some people have ANOTHER antibody that looks enough like a COVID-19 antibody to bind and test positive. It’s inevitable, and built into the test.

Starting Gently

So, let’s pick some numbers for our example. They are guesstimates, but they aren’t far off what a real life test and real-life situation in Alberta will be like in 2020.

That’s all you need. With these assumptions, we can now use Bayes’ theorem. Don’t worry — if you can multiply and divide with a calculator, you can understand this.

The colours I’ve used stay consistent throughout, so you can see which numbers go where.

The equation–don’t panic

Here’s Bayes’ Theorem:

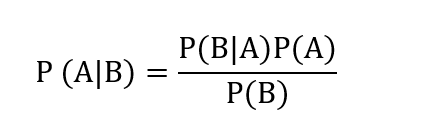
Don’t get scared by the notation. (A | B) just means “Chance of A being true if B is true.” And P (B|A) means “chance of B being true if A is true.” P(A) means “chance of A being true all on its own,” and so on.

In case you have traumatic memories of variables from high school math, we’ll quickly substitute in real words so we know what we mean:

If you write this out in English, you’re saying:

“The chance of the patient truly being immune if they have a positive test is equal to: Chance of a True positive x Chance of truly being immune, all divided by the chance of having a positive test (true positives and false positives).”

Plugging in our colour-coded values

We’ve already seen most of these values already. Here they are colour-coded again like above:

How many total positives will we get?

And now here’s the last bit we need to figure out. It takes a bit of simple math. We want to know what the chance of having a positive test is (all positives, true and false):

Notice that the light blue and dark blue numbers must ALWAYS add up to 100%, since you either have the antibodies, or you don’t. If you raise one number, you lower it by the same amount.

So, this tells us that with this test, and that 15% of the population with antibodies, 18.5% of our tests are going to be positive: almost 1 in 5 tests will be positive! That’s good news, right? We can get 20% of our workforce back to work.

Well, Bayes’ theorem has some bad news.

Finishing the calculation

This is the equation we started with, with the numbers plugged in:

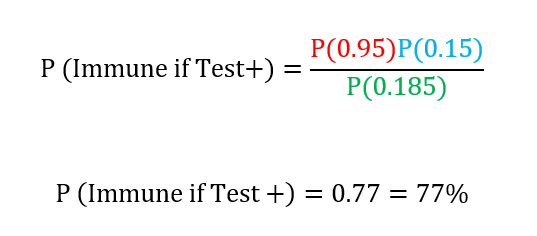
So, if you test positive, you still only have a 3 in 4 chance of truly having antibodies. Put another way, 1 in 4 people that you sent back to work would actually turn out not to be immune.

Now, is that good enough? Or is it enough to start spread of the virus again at unacceptable levels? I don’t know–but it should show you why tests can’t just be ordered willy-nilly, and when you hear that a test is “95% accurate” that doesn’t translate into “only a 1 in 20 chance of giving you the wrong answer.”

You probably wouldn’t tolerate that level of false positive for, say, nursing home workers. Or health care workers. Maybe if you’re working construction, or sitting in an office doing spreadsheets, it might be acceptable.

Playing with the numbers

Let’s play with the numbers a bit. Maybe we just need a better test? Let’s leave aside the question of whether we CAN make an antibody test this good–let’s give it a 99% success rate–99% of positives are true positives.

I won’t bore you with the math again, but the numbers come out like this:

= 0.99 x 0.15 divided by (0.157) = 94.5%.

So, even with a 99% true positive test, we still clear 5% of people improperly. But, maybe we can accept that?

What happens if the number of immune people rises?

If we increase the “pre-test probability” — the chance that someone has the immunity we’re looking for–beyond 15%, what happens then? Let’s say 30% of the population is immune. Using our 95% accurate test, then, the numbers are:

= 0.95 x 0.3 divided by 0.32 = 89%

So, by doubling the number of immune people we’re looking for, the same test is quite a bit better–now we only have a 1 in 10 chance of sending someone back to work who isn’t immune, instead of 1 in 5 chance.

If we double again to 60% of the population being immune, we get:

= 0.95 x 0.6 divided by 0.59 = 96.6%

That’s a less than 5% chance. Not bad. That’s better than a test 99% accurate when 15% are immune.

So what?

So, what this tells you is that early on in the epidemic (which we are) an antibody/immune test isn’t going to be super helpful. Because the number of immune people is relatively low, even with a test as good as we can expect to make it, we still falsely “clear” a ton of people who aren’t immune. We give them and everyone else a false sense of security.

As things move forward, and more and more people are exposed (over time, “flattening the curve”) then these sorts of tests will become more and more reliable. But unless you have a perfect test (which doesn’t exist in this world) then for now these won’t change a whole lot.

Complicating matters: an exercise for the reader

Now, everything we’ve done here is about positive results: true positives and false positives.

Tests also have a rate of false NEGATIVES. That is, just because you’re told you’re negative, doesn’t necessarily mean you’re TRULY negative. The analysis works exactly the same.

But the true positive rate and the true negative rate aren’t necessarily the same. So you have to check for each test you do. And that’s part of the validation that researchers will have to do before they roll these tests out for widespread use. If we don’t know those numbers, we won’t know how to interpret the results.

Extending these lessons

We can draw some conclusions about medical tests in general from this discussion. Because of Bayes’ theorem, tests are not super helpful if someone is very unlikely to have a condition, or very likely to have a condition.

If they are unlikely, then Bayes’ theorem says they’re more likely to get a false positive than a true positive. And if they’re negative, they’re not that much more unlikely to have it than they were before.

And, if they are very likely, then Bayes’ theorem says that even if they test negative, they’re still likely to have it. And, being told they’re positive doesn’t make us that much more confident that they have it.

So, many tests are most helpful at a mid-range probability. A good example is exercise stress-testing for heart disease.

There’s not much value to stress testing a healthy 20 year old. We know his risk of heart disease is very low. If he tests positive on the treadmill test, we’re probably worrying him and ourselves for nothing, and we’ll end up doing more invasive (and dangerous) tests for little gain. We shouldn’t test him at all.

On the other hand, if you have a 60 year old who has crushing chest pain, a history of smoking, and diabetes, with EKG changes suggesting a massive heart attack, trying to get them on a treadmill (even if you could) is foolish. The test isn’t that good. If it was positive, what have we learned? If it’s negative, are we going to send her home and say, “Don’t worry, the treadmill test is negative”? Hardly.

Treadmill is mostly useful in the middle-range case: someone who’s having a bit of shortness of breath, who’s mid 50s, but a non-smoker, though his father had an early heart attack. That kind of thing. We’re not SUPER suspicious, but we are suspicious enough we can’t just ignore him.

One solution

There’s always a “gold standard” test–that’s the best test we can do for whatever we’re looking at. For coronary artery heart disease, it’s squirting dye into the coronary arteries. If you don’t see a blockage–there’s no blockage there. For appendicitis, it’s having a surgeon cut into the belly and take the appendix and put it under a microscope–you’ll know for sure if it was really appendicitis, or really wasn’t. Gold standards are often invasive, frequently more risky, and more costly in terms of labour/time/money.

So, one way we get around these kinds of problems is to have two tests–a screening test like the antibody one. Then, everyone who tests positive is run through a SECOND test, one that is much more accurate. But, that is usually much more expensive and labour intensive (often the same thing). So, it doesn’t make sense to do it for everyone, but it makes sense to check all the screening test positives so you can try to get around Bayes’ theorem.

The problem in this case is that that’s a lot of tests to verify–it might not be feasible.

Bottom line

So, when you hear about these kinds of tests–and you will, and the media will almost certainly get it wrong, or be confused, because most of the people who go into journalism did not enjoy math!–don’t start clamouring for them. They won’t do what we need and want them to do–yet.

And when they do, you can bet we’ll start using them.

Continue reading at the original source →